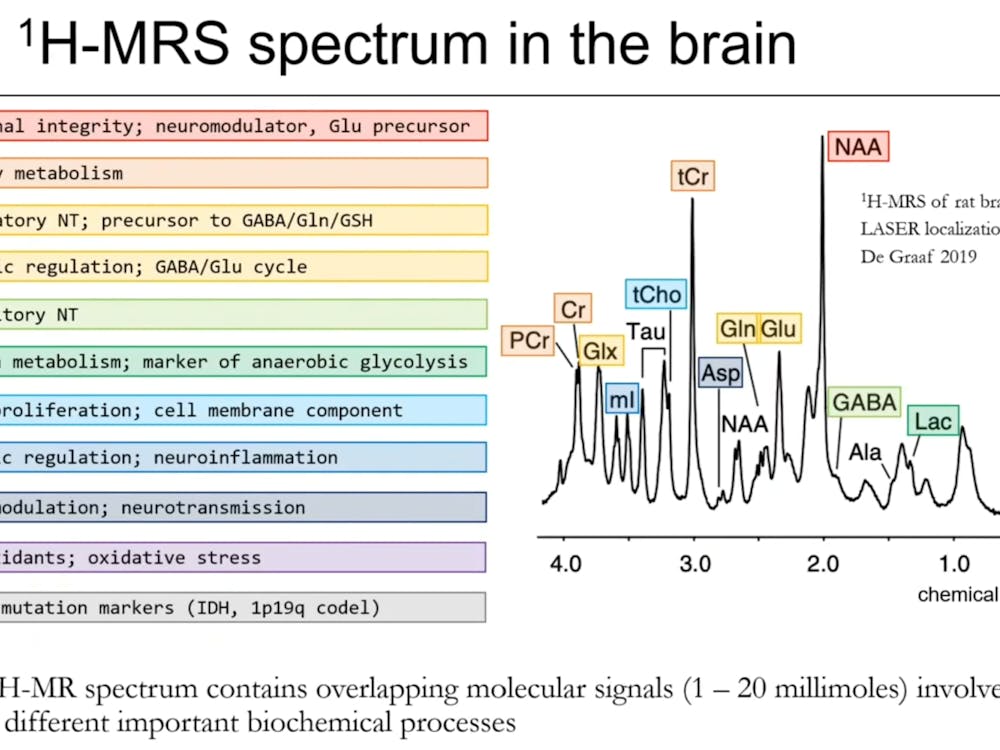
How can we get computers to make decisions like humans? This is one of the foundational questions of neural networks and the rapidly-growing field of artificial intelligence. These research areas rely substantially on large data sets, and that is where the emergence of “big data” has taken place.
Big data exists due to the demand for increased data quantities in order for improved decision making and predictive thinking. Priming these enormous data sets for such usage and extracting underlying patterns and entities is the focus of optimization.
The mathematics and computing techniques at the forefront of these revolutions in data science were the main starts of the 2019 MINDS Symposium on the Foundations of Data Science. The symposium, hosted by Hopkins at Shriver Hall on Wednesday, Nov. 20 was free and open to the public.
Several of the presentations were given by Hopkins professors in the Whiting School of Engineering, and others were delivered by leading professors from other universities.
The talks were divided into sessions, with different sessions focusing on different subfields of data science and mathematical applications. The opening session was centered on the foundations of optimization and the characteristics of big data sets themselves. The second session built on those ideas and focused on the best ways of extracting optimization from the data sets themselves, as well as simply understanding the mathematics behind big data analytics.
A following session developed these ideas and the applicability of big data specifically in neural networks, and the concluding session offered more applications of large data set computing, such as in the emerging field of cryo-electron microscopy and in efforts to understand the networking of the human brain itself.
One of the presenters in the second session, Martin Wainwright, gave a talk titled “From Optimization to Statistical Learning: A View from the Interface.” The talk discussed the problems and occurrences of overfitting that are encountered in the pursuit of optimization. Amidst the complex mathematical formulae and theorems, Wainwright mentioned an epigram by French writer Jean-Baptiste Alphonse Karr.
“The more things change, the more they stay the same,” Wainwright said.
This quote was invoked during a discussion about the revolutions in data science taking place, and how fields or directions pursued momentarily in the past often re-emerge as holding potential solutions encountered in the future.
Wainwright also argued that optimization should occur, but to a limit. He elaborated that after finding the “sweet spot” where optimization of data would be maximized in usage potential, there is too much error, and it is finding this point of least error that is driving many of the mathematical research projects in this highly trending field.
In the session after lunch, Joan Bruna of New York University began with a talk titled “Mathematics of Deep Learning: myths, truths and enigmas.”
This began a more formal interpretation of the problems in optimization as they relate to neural networks and technological applications.
Bruna expressed that we’re still dealing with many of the mathematical theorems and foundations behind the development of such technologies. One of the concepts that he covered was the idea of the “curse of dimensionality.”
“This is where ‘classic’ functional spaces do not play well with the tradeoffs of optimization,” Bruna said.
To avoid these immediate effects of the “curse of dimensionality,” he chose to focus his talk on the simplest neural network family, which is the single hidden layer neural network.
By showing why we must first understand how these neural networks work, without even investigating deep learning right away, Bruna argued that the mathematics of simpler neural networks are foundational to the related application of big data sets in technology and also in mathematical proofing.
Related to mathematical proofs and theorems, Rachel Ward of the University of Texas at Austin gave a talk titled “Concentration Inequalities for Products of Independent Matrices.”
Ward discussed how many of the proofs relating to data set utilization of independent matrices have been by brute-force, and how this has led her to investigate various approaches for a proof to Oja’s algorithm.
Oja’s learning rule is a model of how biological neurons or artificial neural networks change strength in connectivity over time. These changes are what cause “learning” and are inherently fundamental in the study of big data science.
Ward noted that the guiding question of her research is: What would the dream proof of Oja’s rule look like?
It is these sorts of guiding questions and problems of complexity that are propelling the newest revolutions in data science. These problems are being researched at Hopkins, which holds pioneering institutions for researching data science in its mathematical foundations and its technological applications.